Hanbaek Lyu, Assistant Professor of Mathematics, University of Wisconsin–Madison and IFDS faculty, was published in the January 3, 2023 issue of Nature Communications. His article Learning low-rank latent mesoscale structures in networks is summarized below.
Introduction:
We present a new approach to describe low-rank mesoscale structures in networks. We find that many real-world networks possess a small set of `latent motifs’ that effectively approximate most subgraphs at a fixed mesoscale. Our work has applications in network comparison and network denoising.
Content:
Researchers in many fields use networks to encode interactions between entities in complex systems. To study the large-scale behavior of complex systems, it is useful to examine mesoscale structures in networks as building blocks that influence such behavior. In many studies of mesoscale structures, subgraph patterns (i.e., the connection patterns of small sets of nodes) have been studied as building blocks of network structure at various mesoscales. In particular, researchers often identify motifs as k-node subgraph patterns (where k is typically between 3 and 5) of a network. These patterns are unexpectedly more commonthan in a baseline network (which is constructed through a random process). In the last two decades, the study of motifs has yielded insights into networked systems in many areas, including biology, sociology, and economics. However, not much is known about how to use such motifs (or related mesoscale structures), after their discovery, as building blocks to reconstruct a network.
Networks have low-rank subgraph structures
The figure above shows examples of 20-node subgraphs that include a path (in red) that spans the entire subgraph. These subgraphs are subsets of various real-world and synthetic networks. The depicted subgraphs have diverse connection patterns, which depend on the structure of the original network. One of our key findings is that, roughly speaking, thesubgraphs have specific pattern. Specifically, we find that many real-world networks possess a small set of latent motifs that effectively approximate most subgraphs at a fixed mesoscale. The figure below shows “network dictionaries” of 25 latent motifs for Facebook “friendship” networks from the universities UCLA and Caltech Facebook. By using subgraph sampling and nonnegative matrix factorization, we are able to discover these latent motifs.
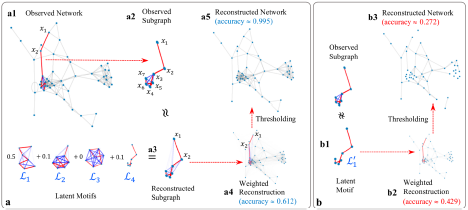
The ability to encode and reconstruct networks using a small set of latent motifs has many applications in network analysis, including network comparison, network denoising, and edge inference. Such low-rank mesoscale structures allow one to reconstruct networks by approximating subgraphs of a network using combinations of latent motifs. In the animation below, we demonstrate our network-reconstruction algorithm using latent motifs. First, we repeatedly sample a k-node subgraph by sampling a path of k nodes. We then use the latent motifs to approximate the sampled subgraph. (See panels a1–a3 in the figure below.) We then replace the original subgraph with the approximated subgraph. By doing this over and over, we gradually form a weighted reconstructed network. The weights indicate how confident we are that the associated edges of the reconstructed network are also edges of the original observed network.
Selecting appropriate latent motifs is essential for our approach. These latent motifs act as building blocks of a network; they help us recreate different parts of it. If we don’t pick an appropriate set of latent motifs, we cannot expect to accurately capture thestructure of a network. This is analogous tousing the correct puzzle pieces toassemble a picture If weuse the wrong pieces, we will assemble a picture that doesn’t match original picture.
Motivating Application: Anomalous-subgraph detection
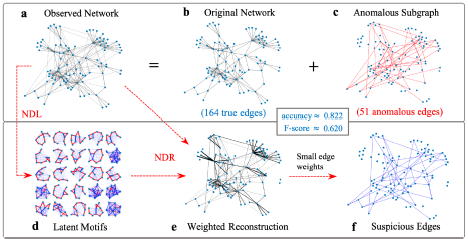
A common problem in network analysis is the detection of anomalous subgraphs of a network. The connection pattern of an anomalous subgraph distinguishes it from the rest of a network. This anomalous-subgraph-detection problem has numerous high-impact applications, including in security, finance, and healthcare.
A simple conceptual framework for anomalous-subgraph detection is the following: Learn “normal subgraph patterns” in an observed network and then detect subgraphs in the observed network that deviate significantly from them. We can turn this high-level idea into a concrete algorithm by using latent motifs and network reconstruction, as the figure above illustrates. From an observed network (panel a), which consists of the original network (panel b) and an anomalous subgraph (panel c), we compute latent motifs (panel d) that can successfully approximate the k-node subgraphs of the observed network. A key observation is that these subgraphs should also describe the normal subgraph patterns of the observed network. Reconstructing the observed network using its latent motifs yields a weighted network (panel e) in which edges with positive and small weights deviate significantly from the normal subgraph patterns, which are captured by the latent motifs. Therefore, it is likely that these edges are anomalous. The suspicious edges (panel f) are the edges in the weighted reconstructed network that have positive weights that are less than a threshold. One can determine the threshold using a small set of known true edges and known anomalous edges. The suspicious edges match well with the anomalous edges (panel c).
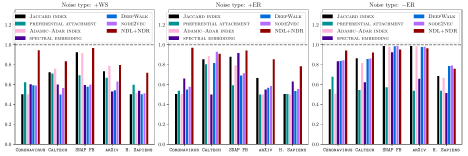
Our method can also be used for “link-prediction” problems, in which one seeks to figure out the most likely new edges given an observed network structure. The reasoning is similar to that for anomalous-subgraph detection. We learn latent motifs from an observed network and use them to reconstruct the network. The edges with the largest weights in the reconstructed network that were non-edges in the observed network are our predictions as the most likely edges. As we show in the figure below, our latent-motif approach is competitive with popular methods for anomalous-subgraph detection and link prediction.
Conclusion
We introduced a mesoscale network structure, which we call latent motifs, that consists of k-node subgraphs that are building blocks of the connected k-node subgraphs of a network. By using combinations of latent motifs, we can approximate k-node subgraphs that are induced by uniformly random k-paths of a network. We also established algorithmically and theoretically that one can accurately approximate a network if one has a dictionary of latent motifs that can accurately approximate mesoscale structures of the network.
Our computational experiments demonstrate that latent motifs can have distinctive network structures and that various social, collaboration, and protein–protein interaction networks have low-rank mesoscale structures, in the sense that a few learned latent motifs are able to reconstruct, infer, and denoise the edges of a network. We hypothesize that such low-rank mesoscale structures are a common feature of networks beyond the examined networks.